本文程序代码来自 《Python深度学习》 第二版的第三章
视频讲解【YouTube】:DL with Python 09. Introduction to Keras and TensorFlow-2: TensorFlow 的第一步
生成数据集
为了方便之后的程序演示过程,首先需要生成特定的线性可分的两类数据,之后再利用 梯度下降 找到一条直线将两类数据分割开来。
这里使用 多元正态分布 分别在不同的中心(期望)处生成两类样本点集的坐标,根据正态分布的分布曲线,越靠近中心处取到值的概率越高,也就是越靠近中心处的点越密集,这样虽然两个点集的范围也有交叠,但大致也是可以用一条直线将两个集合分割开,尽量的使直线两边只有一类点。
首先导入之后需要用的到模块:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt在二维平面上随机生成两群各有 1000 个点的点集,两个点集 negative 与 positive 的中心(期望)分别为 (0,3) 与 (3,0),标准差分别为 (1,0.5) 与 (0.5,1):
num_samples_per_calss = 1000
negative_samples = np.random.multivariate_normal(
mean=[0, 3],
cov=[[1, 0.5], [0.5, 1]],
size=num_samples_per_calss
)
positive_samples = np.random.multivariate_normal(
mean=[3, 0],
cov=[[1, 0.5], [0.5, 1]],
size=num_samples_per_calss
)之后将两个点集垂直的拼接称为一个集合,并使其为 float 类型:
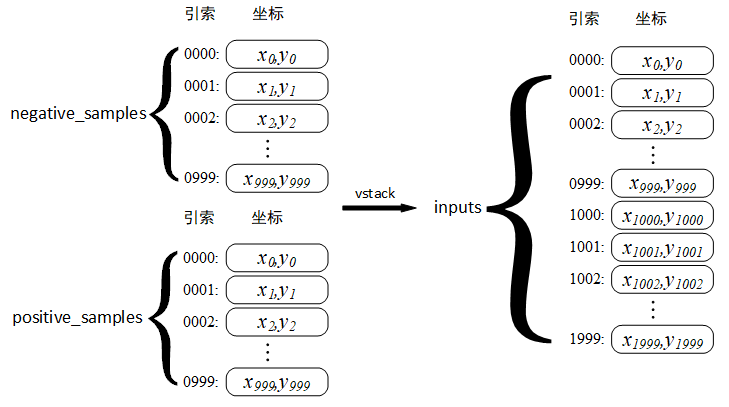
inputs = np.vstack((negative_samples, positive_samples)).astype(np.float32)拼接后的结构如下图所示:
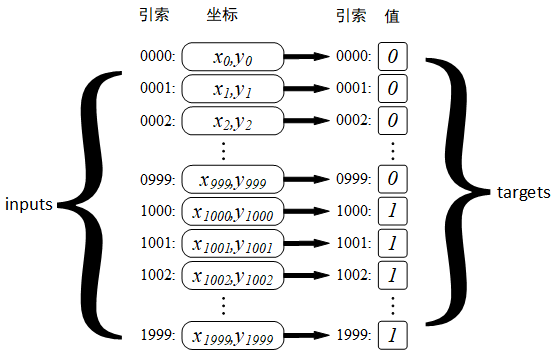
生成两类点集对应的目标值, negative 为 0,positive 为 1 :
targets = np.vstack((
np.zeros((num_samples_per_calss, 1), dtype="float32"),
np.ones((num_samples_per_calss, 1), dtype="float32")
))
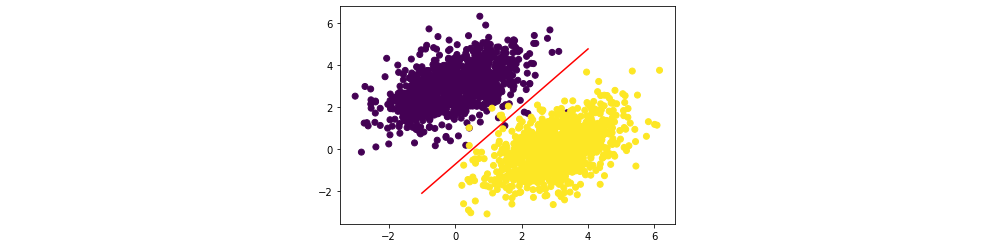
画出点集,negative 为紫色,positive 为黄色:
plt.scatter(inputs[:, 0], inputs[:, 1], c=targets[:, 0])
plt.show()
可以看到,生成的点正如我们所设想的那样大部分聚集在两个中心,越远离中心越稀少,并且在虽然有所交叠,但还是可以大致分出两类点的边界。
创建线性分类器
下面我们就要使用机器学习的方式,运用 梯度下降 得到一条可以尽量分割两类点集的直线。
我们都知道,在二维空间中可以使用 y=kx+l 的形式表示一条直线,我们现在的目标就是通过上面得到的数据点集,令 inputs 为 x,targets 为 y,使程序自行寻找到另外两个参数 k 与 l 。
不过在计算过程中是使用另一种形式 $$w_{0}x+w_{1}y=b$$ 即 $$y=\frac{w_{0}}{w_{1}} x+\frac{b}{w_{1}}$$ 其中 $$k=\frac{w_{0}}{w_{1}}\qquad l=\frac{b}{w_{1}} $$
首先需要设定一个权重张量(矩阵) W,其初始值用随机数填充,以及偏置张量 b,用 0 填充:
input_dim = 2
output_dim = 1
W = tf.Variable(initial_value=tf.random.uniform(shape=(input_dim, output_dim))) # 随机初始权重
b = tf.Variable(initial_value=tf.zeros(shape=(output_dim,)))
由输入(样本值)经过一定的运算得到输出(预测值)的过程就称为前向传播,其中包含参数的全部运算又可以认为是神经网络的模型,此处运算的数学表达式为 $$inputs\cdot W+b$$ 则定义前向传播函数为:
def model(inputs):
return tf.matmul(inputs, W) + b计算输入样本对应的 目标值 与前向传播运算得到的 预测值 之间误差的函数称为 损失函数,计算误差的方式有很多,这里计算的是 均方误差,则定义均方误差损失函数为:
def square_loss(targets, predictions):
per_sample_losses = tf.square(targets - predictions)
return tf.reduce_mean(per_sample_losses)有了损失函数,知道当前参数计算得到的预测值与真实的目标值之间的 “距离”,便可以使用 梯度下降法 对参数进行更新,最快的使预测值接近目标值,由梯度的计算公式 $$\nabla loss(W,b)=\left { \frac{\partial loss}{\partial W},\frac{\partial loss}{\partial b} \right }$$ 更新一次参数的过程就是一次训练的过程:
learning_rate = 0.1 # 学习速率
def training_step(inputs, targets):
with tf.GradientTape() as tape:
predictions = model(inputs)
loss = square_loss(predictions, targets)
# 计算 loss 分别对 W、b 的导数,即计算 loss
grad_loss_wrt_W, grad_loss_wrt_b = tape.gradient(loss, [W, b])
# W = W - grad_loss_wrt_W * learning_rate
W.assign_sub(grad_loss_wrt_W * learning_rate)
# b = b - grad_loss_wrt_b * learning_rate
b.assign_sub(grad_loss_wrt_b * learning_rate)
return loss完成训练
至此,一个简单的线性分类器就已经完成了,接下来我们就可以把最开始生成的样本数据交给刚刚编写的线性分类器令其完成分类,但只是训练一次,更新一次参数是很难很好的完成分类任务的,所以这里我们选择进行 40 次的训练,并输出每次训练的损失:
for step in range(40):
loss = training_step(inputs, targets)
print(f"Loss at step {step:00d}: {loss:.4f}")训练过程的输出如下所示,可以看到第一次训练后预测值与目标值的差距很大,但在之后的过程中他们的差距很快减小。
Loss at step 0: 5.7112
Loss at step 1: 0.3871
Loss at step 2: 0.1542
Loss at step 3: 0.1177
Loss at step 4: 0.1066
Loss at step 5: 0.0992
Loss at step 6: 0.0928
Loss at step 7: 0.0870
Loss at step 8: 0.0817
Loss at step 9: 0.0769
...
Loss at step 24: 0.0381
Loss at step 35: 0.0293
Loss at step 36: 0.0289
Loss at step 37: 0.0285
Loss at step 38: 0.0281
Loss at step 39: 0.0277到此就通过线性分类器找到了一条可以将两类点分割开来的直线,我们可以将这条直线画出来,并且还可以计算出这条直线分割的准确率,看看两类点有是否只在直线的一侧:
# 绘制样本点集
plt.scatter(inputs[:, 0], inputs[:, 1], c=targets[:, 0])
# 绘制分割线
x = np.linspace(-1, 4, 100)
y = - W[0] / W[1] * x + (0.5 - b) / W[1]
plt.plot(x, y, "-r")
plt.show()
# 计算准确率
predictions = np.where(predictions[:, 0] > 0.5, 1, 0)
total = np.sum(targets.reshape(2000) == predictions)
print(f"{total}/2000 = {total / 2000 * 100:.2f}")绘制得到的分割线如下图所示
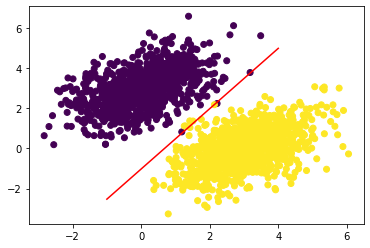
计算得到的准确率为 99.75% ,有 1995 个点很好地分割开来,并且我们可以也可以很直观的看到,两类点基本都分别在分割线的两侧,说明我们的方法是行之有效的。