什么是卷积
不要被 “卷积” 这样不明所以的名字吓到,就像乘法中 a X b 的定义是 a 个 b 相加一样,卷积也仅仅是代表了一种运算规则。对于两个函数,将其中一个函数 反转 后对其进行 平移 操作,每平移一个微小量便令两个函数 对应位置相乘 后 求和(也就是两函数相乘后的面积),求和的结果就是在此处的 卷积,完成从正无穷到负无穷的平移过程便完成了对这两个函数的卷积操作。
也就是说,卷积代表的就是上述的 反转、平移、相乘、求和 的过程。
函数的基本变换
为了方便之后描述运算过程,首先需要对函数的几个基本变换有所了解,这里以有限长离散序列为例,且只讲述反转、平移两种变换,对于无限长、连续函数基本一致,且其他变换请自行搜索学习,这里不再赘述。
假设我们现在有一个有限长的的离散函数序列 g(k),其图像如下图所示,之后变换中所用的序列未加说明均指此序列。
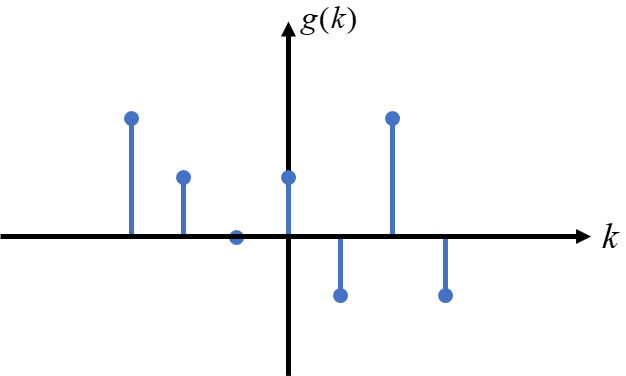
反转变换
序列 g(k) 以 y 轴 为对称轴做轴对称变换得到 g(-k) 的过程称为反转变换。
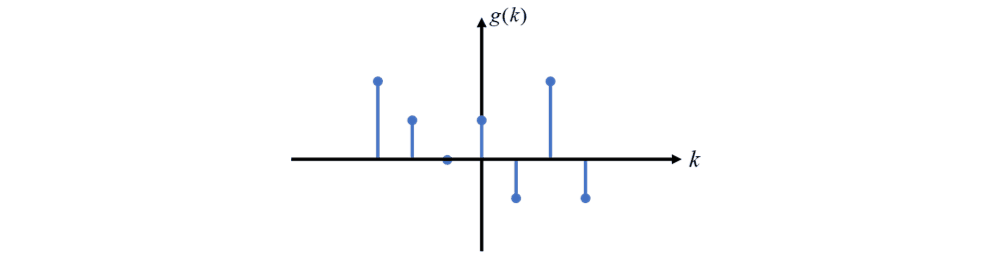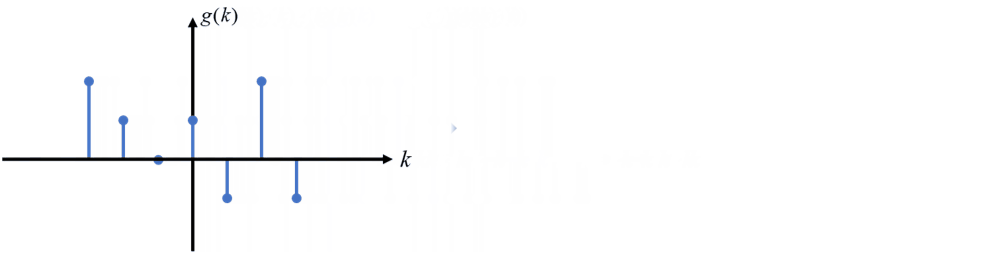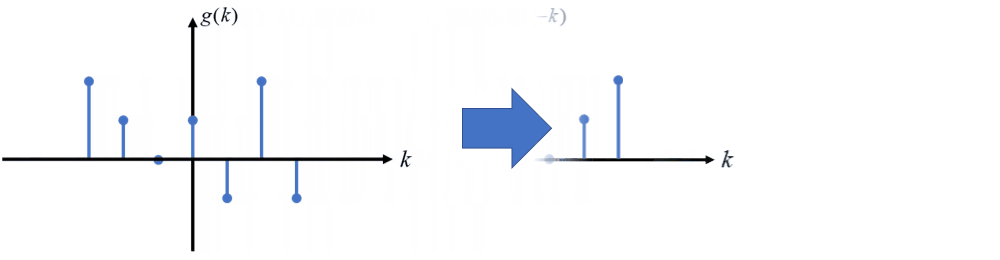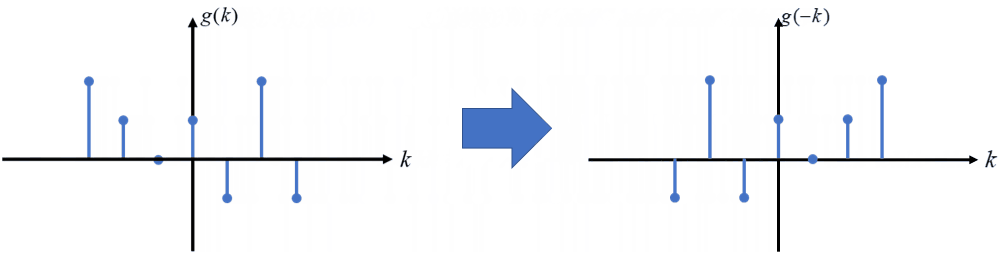
平移变换
序列 g(k+l) 表示在原来的基础上将序列向 右 平移 l 个单位,若为 g(k-l) 则为向 左 平移 l 个单位。
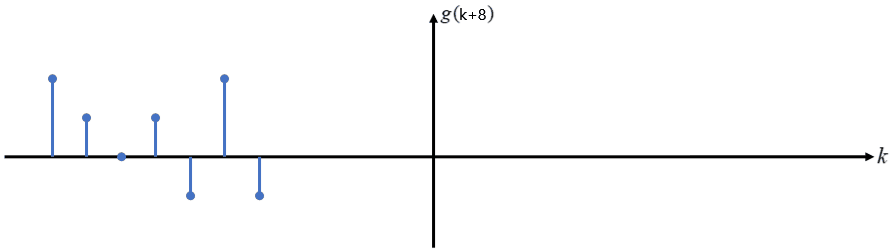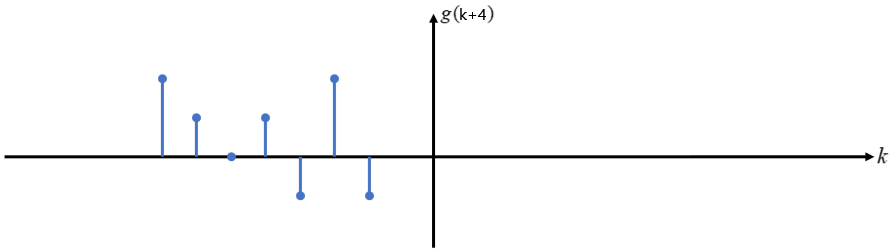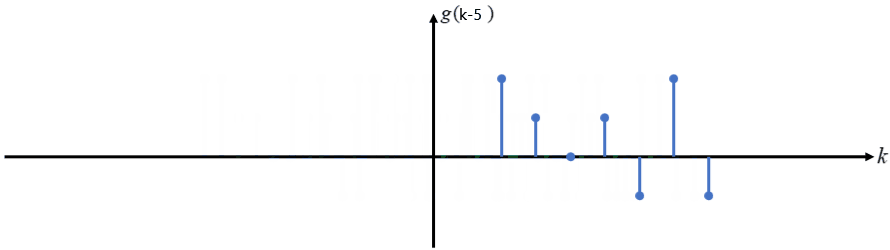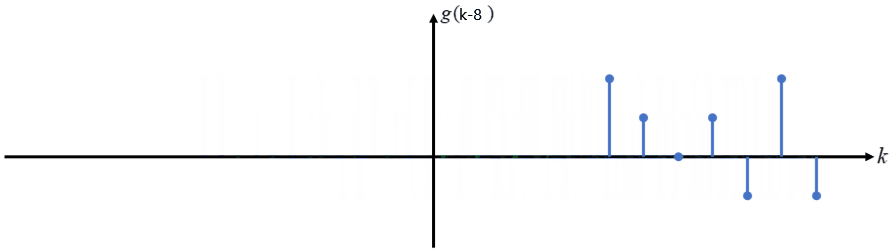
卷积的图解法
为了方便描述与计算,这里选用两个有限长离散序列 f(k) 与 g(k) 来举例,相应的,无限长的与连续的函数也是一样的计算思想。
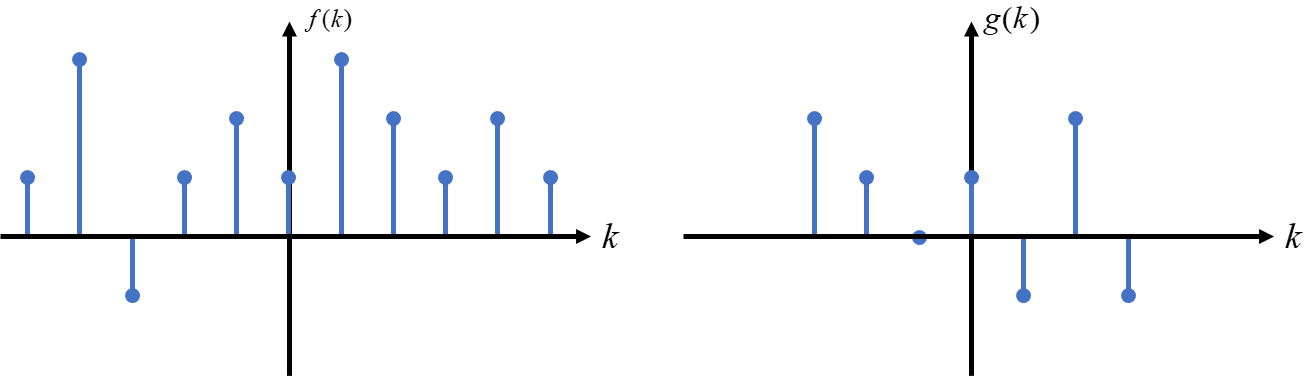
首先将 g(k) 反转得到 g(-k)。
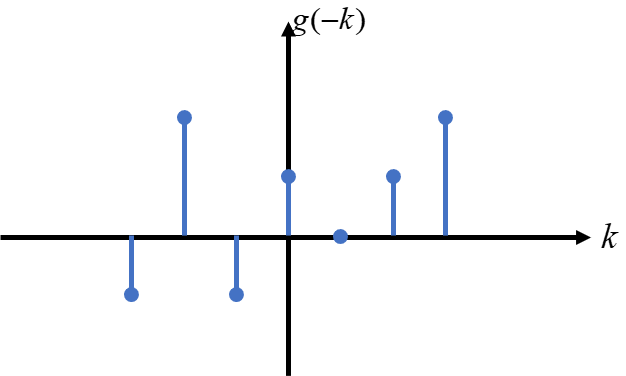
然后将 g(-k) 由负无穷到正无穷平移,即 g(l-k) 其中 l 依次由正无穷至负无穷取值,l 每取一次值不同的值后 g(l-k) 与 f(k) 对应相乘且累加求和一次,则以 l 为自变量,每次求和得到的结果为 因变量 得到的对应关系即为 f(k) 与 g(k) 卷积的结果 h(l)。
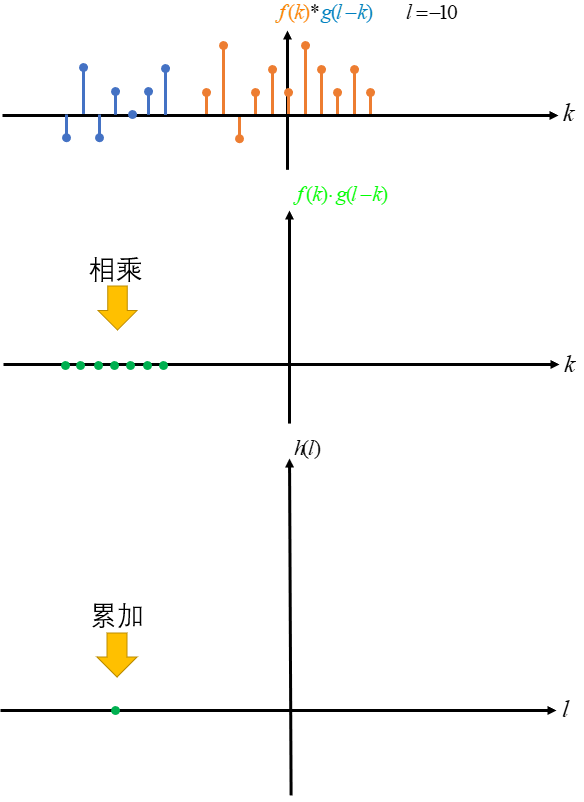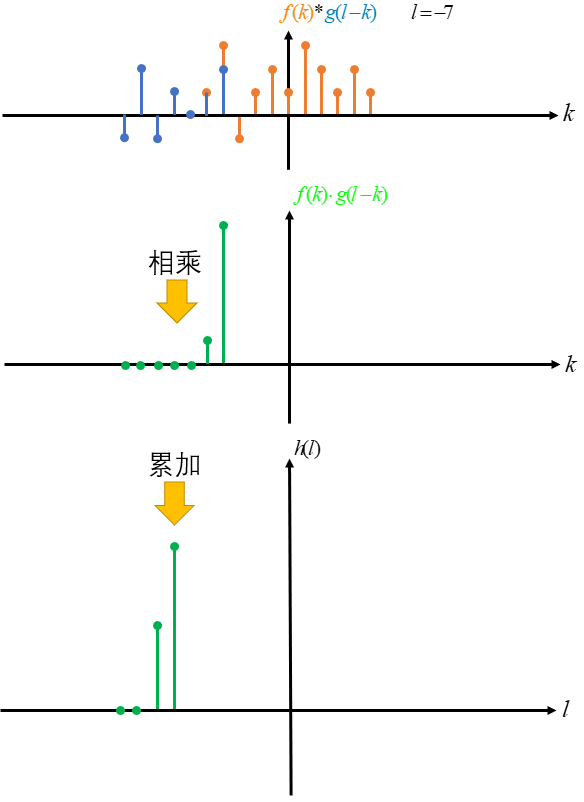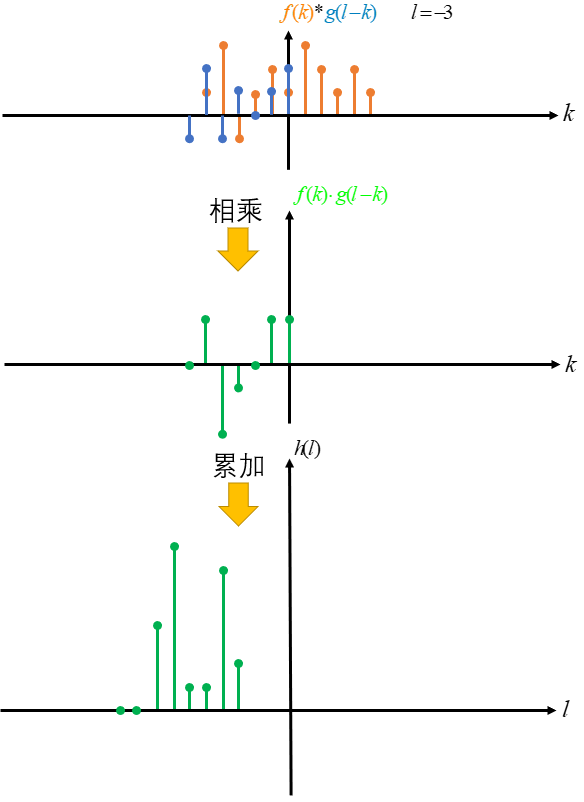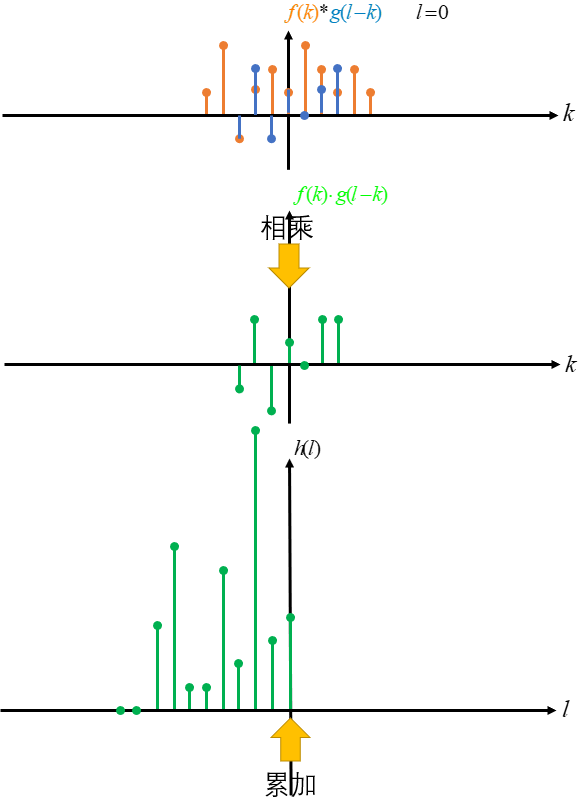
这里只演示了由负无穷至 0 的卷积过程,其他部分是一样的
(才不是因为动画太难做了
卷积的定义
对于严谨的定义,这里直接引用了维基百科中对卷积的描述。
https://zh.wikipedia.org/wiki/%E5%8D%B7%E7%A7%AF
设:


可以证明,关于几乎所有的 







对于定义在整数 

![(f*g)[n]\ \ {\stackrel {\mathrm {def} }{=}}\ \sum _{m=-\infty }^{\infty }{f[m]g[n-m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24eeb66855fb4048d42b33fc6727fdabf6068a27)
这里一样把函数定义域以外的值当成零,所以可以扩展函数到所有整数上(如果本来不是的话)。
当 ![g[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c5e1d771a2385e9aeb71838a40425bb07c89525)

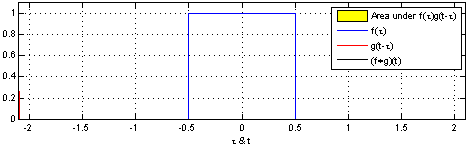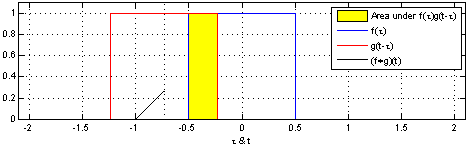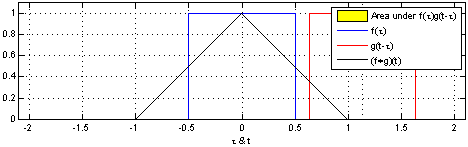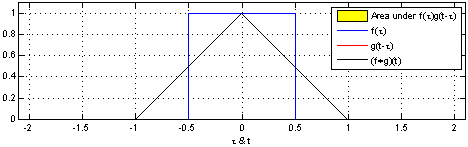
 反射,接着平移”t”,成为
反射,接着平移”t”,成为  。那么重叠部分的面积就相当于”t”处的卷积,其中横坐标代表待变量
。那么重叠部分的面积就相当于”t”处的卷积,其中横坐标代表待变量  以及新函数
以及新函数  的自变量”t”。
的自变量”t”。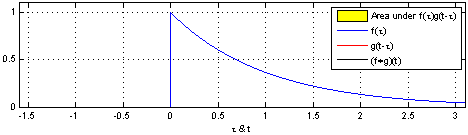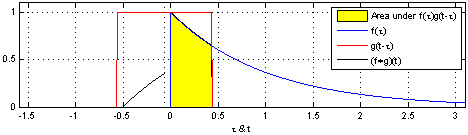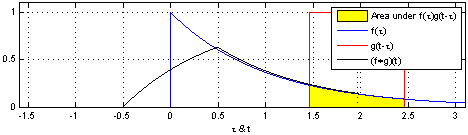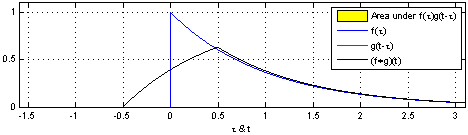
推荐阅读/观看
(卷积不用反转?!)【知乎】如何通俗易懂地解释卷积?
【Bilibili】十分钟搞懂【卷积】


![=\sum _{m=-\infty }^{\infty }f[n-m]\,g[m].](https://wikimedia.org/api/rest_v1/media/math/render/svg/f067498b1393be11cf4cecfb08f3096f14bdce59)
![(f*g)[n]=\sum _{m=-M}^{M}f[n-m]g[m].](https://wikimedia.org/api/rest_v1/media/math/render/svg/fddacde29cbcb3c6fca263493335c31a4d2ebce2)